Side Quests
Searching for history tends to strongly pull you further back in time than you planned. In this case, I found myself reading about Galileo’s improvements to calculating devices for canons.
A Great Book
There are only a few books which cover the history of computing in sufficient technical detail for my purposes. Some, like ENIAC in Action delve deep into a single machine. This is useful, since those machines have key innovations that I want to follow.
Others are more general histories of computing, with less detail, but put various notable machines into a timeline, and describe what unique features put them on that list. I’m finding this book, A History of Computing Technology to be a wellspring of fresh knowledge which expands my horizons.
(Since Wiley objects to having their book lent out by libraries, you may have to pay extortionary prices for a book which hasn’t been updated in almost 30 years. Try your local library, and don’t forget to ask for “interlibrary lending” requests. Or you can try the used book market where it can be had for 1/10th Wiley’s ransom demand.)
But be aware that general histories will have information from a much wider time period than you might be interested in. In this case, the book starts with numbering systems and continues forward in time.
Such a book can pull you aside quite easily, and show you a topic which is so captivating that you have to just follow it down that rabbit hole.
Canons and Calculations
Which is how you get to today’s topic, only tangentially related to how the modern computer architecture came to be.
I set aside a couple of hours to read more of this book. And I wanted to avoid digital things, so I hunted through the pre-electric era material. I became fascinated by the methods and tools being used in the Medieval times (if that’s the correct name). Calculation was done by measuring things. Builders and sailors needed to make particular calculations which occurred frequently in their trades. Navigators on ships far from land had to master arcane knowledge of the stars, and be able to pinpoint date, time, lattitude, and longitude of the ship or all hands could be lost.
The devices they created were somewhat simple looking, but were carefully developed over long periods of time to perform multiple different tasks with a single device. I learned that the “quadrant” was used for multiple different calculations involving the stars. (The name, quadrant, was applied because it was a quarter of a circle. I assume – but haven’t checked – that the “sextant” is one-sixth of a circle.) The most notable thing, or at least what leaped out to me, was that these instruments had multiple scales inscribed on them with each highly accurate scale being used for different sorts of calculations.
Let me make a personal historical note: My first calculator was a slide rule. Yes, I’m older than a calculator. Or at least any mass-produced calculator at a price my family could afford. On the other hand, a slide rule was a few dollars ($24 US in today’s money), and could do all the things I needed. Squares, Cubes, Square Roots, Cube Roots, and probably more things that I never learned how to do. So when I see an instrument with scales on them, I immediately attach that to my memories of doing physics with a slide rule. Younger readers probably don’t have that visceral connection, so it may be hard to grasp the true value of these ancient ways of computing. But I’ll try to at least link it to the modern computer, and ENIAC specifically. The pictures should help.
ENIAC was approved to meet an urgent war-time need. The US Army needed accurate ballistic tables in order to accurately aim their artillery and do the most damage for the least effort and cost. But these “firing tables” took weeks to compile, due to the many, many repetitive calculations involved. ENIAC was able to automate that process and produce more accurate tables in days.
Back In The Day
In medieval times (say 1500s, 1600s), the main military weapon was a canon. These revolutionized war, but the gunners still had the same problem as the Allies in WWII; how to accurately aim the canon? Obviously, you want the long axis of the canon to be in line with the destination target. But how far away is that target? Basic ballistics (and “equations of motion” from physics) will tell you that the maximum range is obtained when the gun points up at 45 degrees from horizontal. Gunners could (and did) make “ranging shots” to see if their canonballs went too far or not far enough. This obviously wasted ammunition and powder, so a solution was sought.
They could do test-firings of each gun after it was built, and make note of the range for different “muzzle elevations”. Then in the field, a gunner could see that to hit a target 1000 yards away, they would need to set the barrel angle at, say, 15 degrees. So they developed a simple device to help with this.
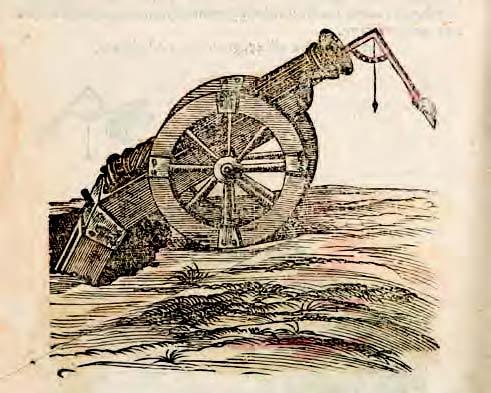
Tartaglia, La Nova Scientia, ca. 1550
The “gunner’s compass” (see Notes) looked like a carpenter’s framing square, with two straight legs set at 90 degrees to each other. One leg was longer, so it could reach down the barrel of the canon. Between the two legs was a curved scale, and from the point of the square, a plumb bob was hung (just a string with a heavy weight, to indicate where “down” was.) As the barrel of the gun was raised and lowered with the compass in place, the string of the plumb bob would cross different locations on the curved scale. That scale was marked off with 12 equally-spaced “points”.
With the canon pointed straight up, the bob would hang at the end of the scale closest to the barrel, and that was marked as “point 12” (see Notes). At 45 degrees the bob would be over “point 6.” To set the gun for that 1000 yard shot, you’d use 15 degrees, which was 1/3 of 45, so you’d tilt it until it read “point 2”.
(And a bit of trivia: Europeans at the time did not use the number 0, and didn’t consider it a “real” or “valid” one, so they left this spot blank. When the gun was pointed horizontally, the plumb bob was at the other end of the curved scale, and that spot had no number listed. This is “point blank”, and where that bit of English idiom comes from.)
Enter Galileo
All of this is fine, but it doesn’t take into account all the variables required for accurate fire. And in a war, a missed shot is worse than no shot because you’ve used up finite resources. (This is why disrupting supply chains can win or lose wars, and why militaries spend so much time and effort on “logistics”. More wars were lost by storekeepers than by soldiers.)
Some of the variables: the canonballs were different sizes, densities (and therefore weights), and the amount of power used would determine the force applied to the ball. What Galileo did is improve mechanical calculating devices to measure these various factors (like making the arms of the compass pivot forming a caliper to measure the diameter of the ball), and included tables carved into them listing the compensations needed for amount of powder, etc. This meant that with Galileo’s improved device, gunners had everything they needed for pinpoint accuracy in a form they could easily carry.
This device was eventually named the “sector”. Here’s an image 1 of one Galileo had made before he published his book 2 on the subject, “Operations of the Geometric and Military Compass”, 1606.
Note that this is simply one configuration of the instrument, showing it as a gunner’s compass. There were attachments and such to enable other uses of the device as mentioned above.
Back To Our Regularly-Scheduled Program
So how is this related – even tangentially – to ENIAC? Well, I mentioned above that Galileo and Eckert/Mauchly were solving the same problem. And the same thing was happening: the tools were too inexact and hard to use for the time. And just as Galileo was able to get better results by using more of the variables at play (power, shot size, etc.), so ENIAC was able to produce tables using more variables than those previous human “computors” were able to manage.
There is so much more in that chapter which is calling to me. As a slide-rule user, I can see the linkage between numbers etched on a stick turning into multiple devices using logarithms as their base for functionality, to two such sticks and a sliding one used for centuries as the primary calculating tool, and finally to ENIAC, whose “function table” was, at times, a table of logarithms.
More importantly for the development of any new technology, the inventors and creators were immersed in these old ways, and new things tended to be better/faster/cheaper versions of those old things. Those new things change the way people think about solving problems, and they start using the new technology in new ways, eventually modifying it away from being old wine in a new skin.
Notes
“Compass”
Not a direction-finding compass, but a geometry compass.
Remember when you were in school, and had to draw a cirle with a radius of 3cm? You’d get out that mechanical contraption with two legs, a point on one end, and a small bit of pencil on the other. Then set their distance using a ruler, place the point where you want the circle’s center to be, and pivot around that. The pencil on the other end draws out the circle you wanted.
In olden times, you would make calculations by setting a compass (with two points, no pencil) using one of the (many) scales on the device, and then using that distance to measure along another scale, with the result you desired read out from this new scale. It’s complicated if you’ve never used logarithms to multiply numbers by adding. Along side my slide rule was a thick book called “table of logarithms”. That was the primary toolset of engineers and scientists.
“Base-12 Systems”
The use of 12-based arithmetic was so convenient in many ways for the pre-Industrial world that 12 and 60 based counting systems were used across the planet. The reasons are too long for this note, but do help you understand why they exist and hang on even today.
-
Image copyright Sage Ross, CC-BY-SA & GNU Free Documentation License ↩